Forces Acting On A Door Hinge

The forces that the door exerts on its hinges can be found by simply reversing the directions of the forces that the hinges exert on the door. An unknown force. The weight of the door which can be considered as acting at the center of gravity of the door.

entryway simple marble floor design example oil based paint on panel molding walls express roofing weymouth ma exterior color schemes red roof fj40 roof top tent fiddler on the roof fans flaxpod roof colour fix my sliding door lutz

The Physics Of Our Back Gate Scienceblogs

Determine The Moment Of The Force F About The Door Hinges At A And B Youtube

Solved A Uniform Door Hangs By Two Hinges As Shown In The Chegg Com

Uniform Door High Wide Hung Two Hinges Cm Top Cm Bottom Hinge

31 Physics Rigid Body Dynamics Force By Hinges On A Door By Ashish Arora Ga Youtube

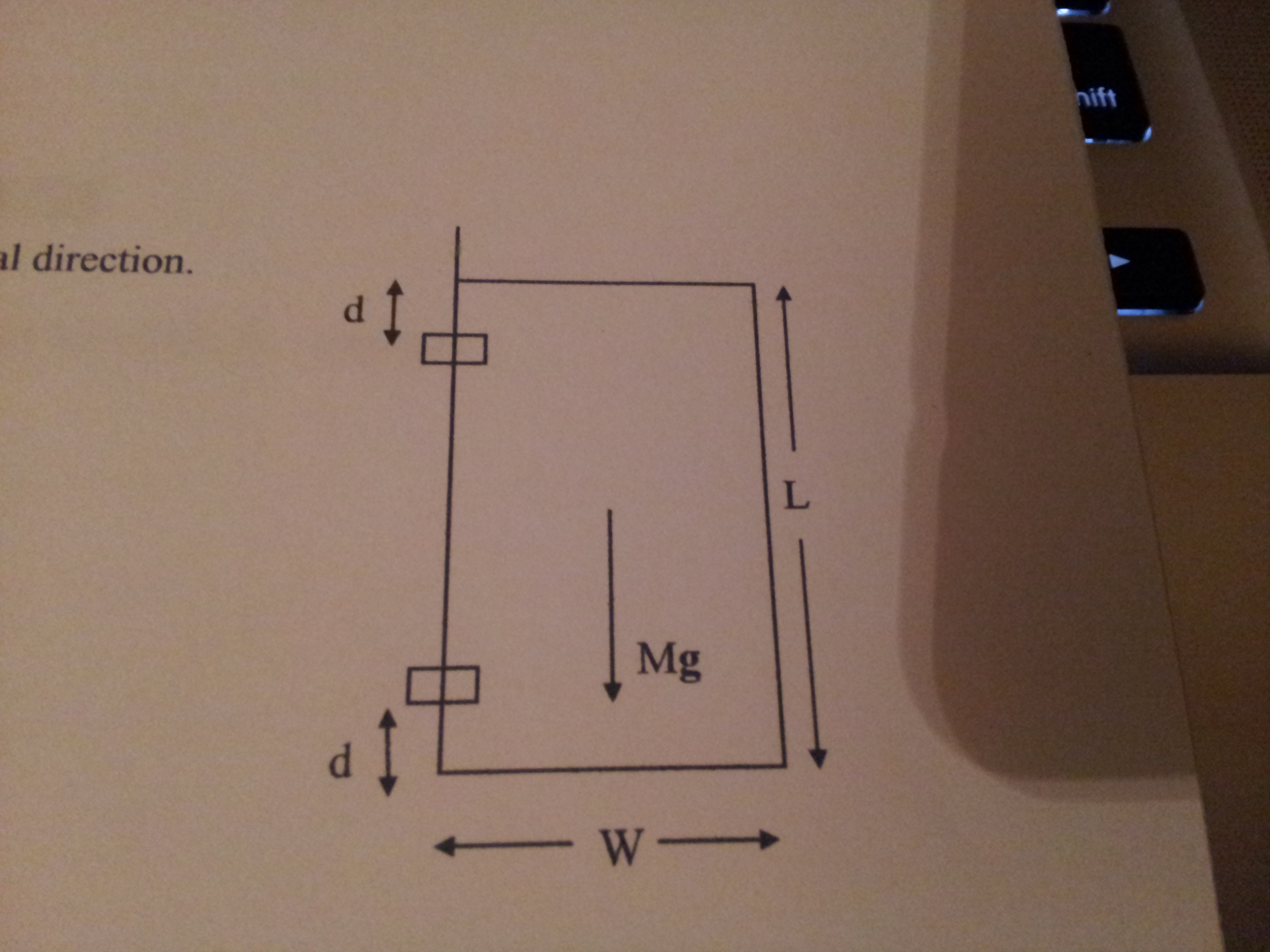
12 2 Examples Of Static Equilibrium University Physics Volume 1

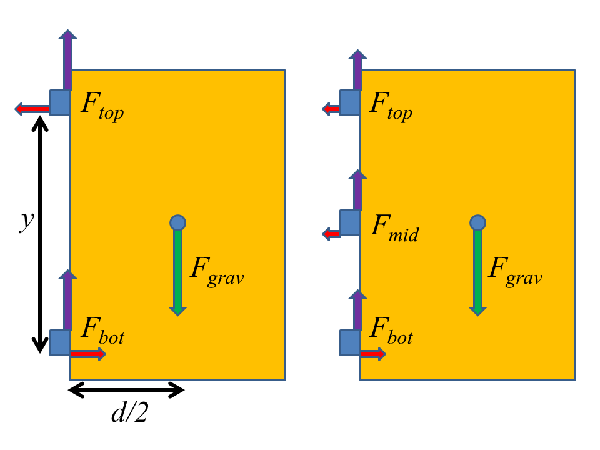
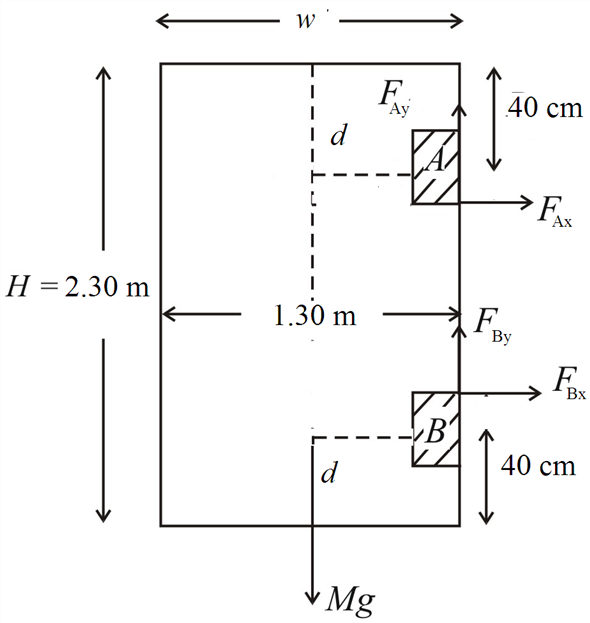
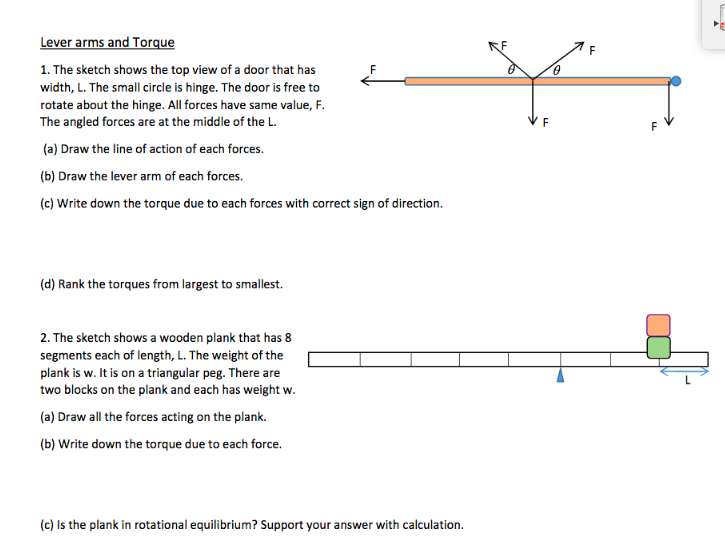
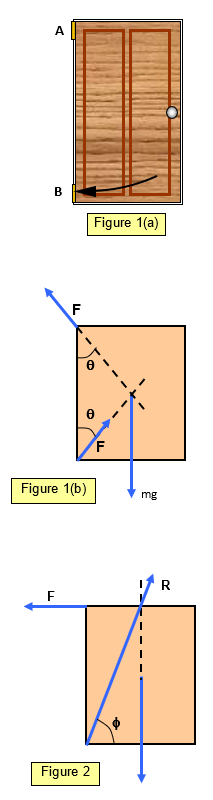
For simplicity the door is shown as completely uniform the hinges a and b are symmetrical placed at the corners of the door and each supports half the weight of the door.

Forces acting on a door hinge.

And the known weight. It tries to turn it about a horizontal axis. Forces on the door. Does its weight cause any torque about this axis.

And the forces at each hinge. This is different from the global null bending moment equation which considers all forces to either side of the hinge. Rigid bodies sys of forces 41 of 47 forces and moments example 7 duration. The force at each hinge can be broken up into a vertic view the full answer.

Let s say that the door is uniform in density weight is open it is not moving or being touched the hinges are all connected to the frame and door leveled and are not offset in distance from the frame or door more than their own thickness and when you ask about the forces acting upon each hinge you are asking about the forces felt. Does the weight try to turn the door about a vertical axis. All of those cause torques about. Randall manteufel 2 765 views.

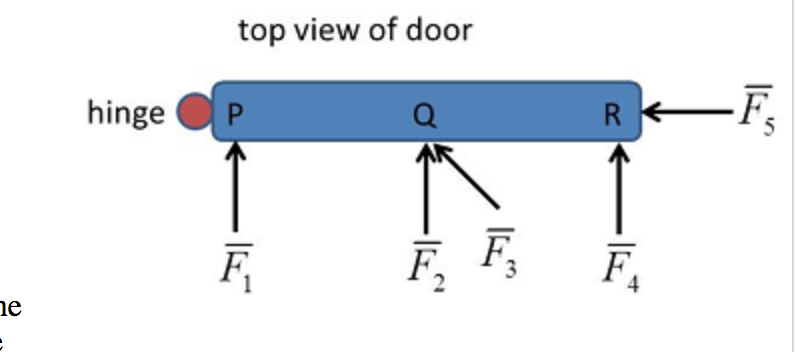
I have been attempting to solve a question where there is a point force acting on the hinge of a beam. There are several forces on the door. Let me make a few assumptions about your question first. To find the torque t door generated by all the forces acting on the door and attachments.

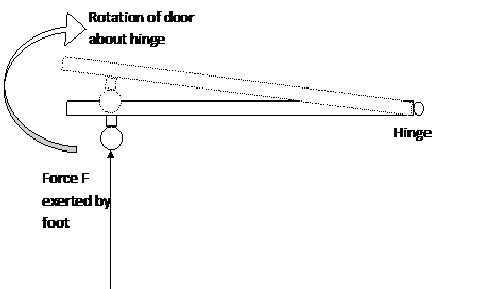
Here is the problem. A door is hinged at one end and is free to rotate about a vertical axis. 3d hanging door rigid body equilibrium spr18 duration. See the picture below.

The forces f in each hinge are equal. Hence our task is to find the forces from the hinges on the door. An unknown force. Figure 1 a shows a door and the forces on the door are shown in figures 1 b.

Gasket forces the force of the door against a sealing gasket if one is present is an out of plane horizontal stress on the hinges. Consider potential shock loads when choosing hinge and door. Three forces act on the door slab. Multiply the distance from the hinge to the center of gravity of the door d 1 by cos θ and by the.